Uzay kafes sistemler doğru eksenli çubukların rijit bir sistem teşkil edecek şekilde sürtünmesiz mafsallarla uçlarından birbirlerine bağlanmasıyla oluşurlar. Uzay kafes sistemlerin temel prensipleri, düzlem kafes sistemlerin temel prensipleri ile aynıdır. Fark kafes sistemin uzayda kurulmuş olmasıdır.
Uzay Kafes Sistemler
•Kafes sistemlerdeki çubuk elemanları uçları mafsallı ve mafsallar arasında herhangi bir kuvvet etkimediğinden, bu elemanlarda sadece eksenel normal kuvvet oluşur, moment etkisi oluşmaz.
•Çubuklarda eksenel normal kuvvet oluşması çubuklara gelen kuvvetlerin hesaplanmasında kolaylık sağlar.
•Uygulamada, kafes sistemler İçin yapılan kabullerden saplamalar olur düğüm noktaları tam olarak mafsal şeklinde imal edilmez ve veya kuvvetler tam olarak düğüm noktalarına etkiyemez, Bu durumlarda çubuklarda eksenel kuvvetlerin yanında, ikinci derece etkiler adı verilen, moment etkileri de oluşur. Bu etkileri mümkün olduğunca küçük tutabilmek İçin düğüm noktalarında birleşen elemanların eksenlerinin bir noktada kesişmeleri sağlanır
UZAY KAFES SİSTEMLERİN KULLANIM ALANLARI
•Fabrika ve depo binaları,
•Uçak hangarı, terminal binaları, otopark ve benzinlik
istasyonu
•Alışveriş merkezleri,
•Spor salonu, kapalı yüzme havuzu, tenis kortu
•Stadyum
•Sinema, tiyatro, konferans salonları, gösteri merkezleri,
•Üst ve tüp geçitler,köprüler…
UZAY KAFES SİSTEMLERİN KURULUŞ ŞEKİLLERİ
Kendi içinde tam bağlı kafes sistemler
Bu tip kafes sistemler kendi içinde bağlı rijit cisim gibi işlem görür. Bu şekilde teşkil edilen sistemin serbestlik derecesi altıdır.
Mesnetleri ile tam bağlı sistemler
Bu tip kafes sistemler ise kendi içinde tam bağlı olmayıp ancak bağlandığı zaman rijittirler.
Uzay kafes sistemler yukarıda bahsedilen sınıflamanın dışında düzlem kafes sistemlerde
olduğu basit, bileşik ve karmaşık olmak üzere üç gruba ayrılırlar.
BASİT KAFES SİSTEMLER
Basit kafes sistemler: Uzay kafes sistemlerinin en basit formu olan bu sistem rijittir. Bu dörtyüzlü düzlemdeki temel üçgenin karşılığıdır. Bu şekilde elde edilen sistem kendi içinde rijittir ve serbestlik derecesi altıdır. Bu sistemler uygun bağlar ile bağlanırlar. Bu bağların kafes sistem teorisine uygun olması için düğün noktalarında bulunması gerekir. Aksi halde sistem, kafes sistem kabul edilmez.
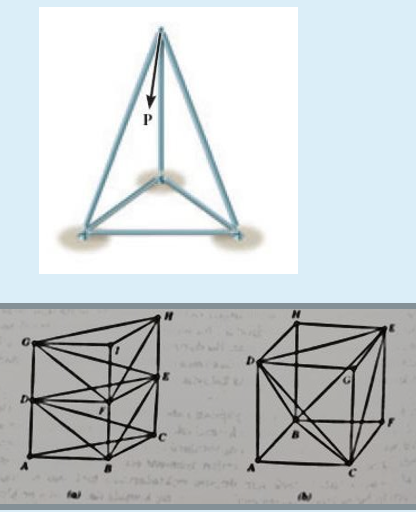
c: çubuk sayısı
d: düğüm noktası sayısı
Çubuk sayısı ve düğüm noktası arasındaki bağıntı
c=3d-6
Basit kafes sistemler dörtyüzlüden başlamadan da kurulabilir. Dörtyüzlü yerine sabit bir temelden de başlanılabilir. Bu şekilde kurulan kafes sistemler ancak mesnetleri ile rijittirler.
Mesnetleri ile bağlı kafes sistemlerde, her düğüm noktası üç çubuk ile teşkil edilip bir başlangıç dörtyüzlüsü bulunmadığından, çubuk sayısı ile düğüm noktası arasındaki bağıntı: c=3d
şeklindedir. Bağıntıda temeldeki bağlantı noktaları düğüm noktaları olarak sayılmayacaktır. Kendi içinde tam bağlı kafes sistemler için aynı sonuç elde edilir. Mesnetleri ile birlikte rijit sistemler için tam bağlılık şartı olarak
s+c=3d bağıntısı da kullanılır. Burada; s, mesnetlerdeki bilinmeyenleri statik değerleri ve d’nin hesabında mesnet noktaları da göz önüne alınacaktır.
Uzay kafes sistemlerde bir nokta oluşturulurken kullanılan üç çubuğun bir düzlemde bulunmaması gerekir. D noktası ABC düzlemine dik şekilde az da olsa hareket eder. Dolayısıyla D noktasının uzayda bağlanması yetersizdir.
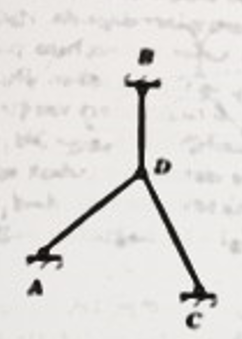
Üç çubuğun düzleminde olmayan bir kuvvet düğüm noktasına etki ettirildiğinde kuvvetin düzleme dik bileşenini karşılayacak çubuk yoktur.
Çubuk kuvvetlerinin hesabı için çubuklardaki şekil değiştirmelerin göz önüne alınması gerekir. Sadece denge denklemleriyle çözülemez.
BİLEŞİK KAFES SİSTEMLER
Bileşik kafes sistemler, birden fazla basit kafes sistemin çeşitli şekillerde rijit bir sistem oluşturacak şekilde bağlanması ile elde edilir.
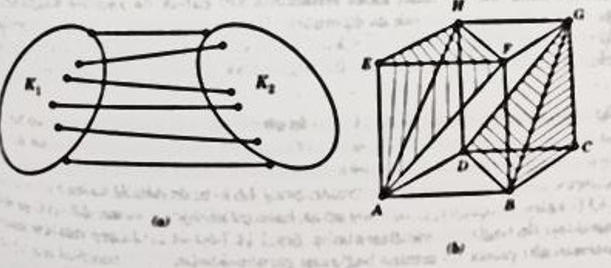
Kafes sistemlerden birinin diğerine göre serbestlik derecesi altı olduğundan altı serbestlik derecesini yok etme yollarından biri altı çubuk kullanmaktır.
İki kafes sistem altı çubuk ile birleştirilirken altı çubuk bir eksine kesmemeli veya bir kısmı kesip diğerleri paralel olmamalıdır. İki üçgen düzlem kafes sistem uzayda altı çubuk ile birleştirilerek birleşik uzay sistemi elde edilebilir.
Bir basit kafes sistem altı çubuk ile başka bir kafes sisteme bağlamak yerine zemine bağlayarak birleşik kafes sistem elde edilebilir.
Mesnetleri ile bağlı basit kafes sistem aynı zamanda basit kafes sisteminin çubuklar İle bağlanmış birleşik kafes sistem olabilir.
İki kafes sistem birbirine bir düğüm noktası ortak hale getirip ve üç çubuk eklenerek bağlanabilir.
KARMAŞIK KAFES SİSTEMLER
Karmaşık kafes sistemlerinin kuruluş biçimleri belirli bir kurala uymazlar. Genel olarak basit veya birleşik kafes sistemlerinde bazı çubukların yerleri değiştirilerek elde edilir. Uygulamada bütün çubukların kafes sistemin dış yüzeyinde toplandığı içinden hiçbir çubuk geçmeyen kafes sistemler çok kullanılır.







